Reach the dew point faster, easier and with greater precision
Numerous industrial and laboratory applications make it necessary to use an airflow with an exactly defined moisture content. Examples for this are sensor calibrations, welding processes, cleanroom technology, fuel cells or the wide field of metal surface treatments. With DewCal®, an absolute working moisture system is now available, with which it is possible to have the dew points of gasses adjusted and controlled very fast.
Fully calibrated humidifying systems are characterized in that the degree of moisture (dew point) is determined on the basis of elementary physical parameters such as the temperature, pressure or the flow rate. This is the reason why the DewCal® is purely based on the precise measuring of the gas temperature and flow rate. A module in the compactly designed system ensures that the vapour flow comes into contact with an exactly tempered wall – and therefore the adjustment of an exactly defined saturation vapour pressure for a certain temperature. This enables the same conditions to be obtained in the DewCal® as are used in the calibration vessels for moisture sensors. This means that DewCal® provides a fully calibrated dew point with a higher long-term stability and deviation from the adjusted dew point which is clearly lower than 1 K.
Its functional principle also enables the system which was developed by Falk Steuerungssysteme GmbH to not only generate water but also calibrated vapour densities or other fluids – namely those that have a comparable vapour pressure curve. Three examples of this are carbon tetrachloride, ethanol and acetone.
 The tempered mixing unit is situated above the vaporizer. The fast and precisely controllable dryer and moist gasses ratio ensures exactly defined atmospheres
The tempered mixing unit is situated above the vaporizer. The fast and precisely controllable dryer and moist gasses ratio ensures exactly defined atmospheresSystem design
With the DewCal®, the gas is initially directed through the water vapour. This is generated in a vaporizer at a temperature which is selected via an operating program. The process gas which streams in over the surface of the fluid is somewhat saturated and leaves the room in the direction of the condenser which has a lower temperature – which is exactly held by the control system –. This results in the water vapour which is excess for this temperature condensing – and the gas subsequently flows to the mixing unit with an absolutely defined and therefore precise dew point.
The monitoring and evaluation of the correcting variables for the vaporizer and the condenser guarantee optimal working conditions with the assistance of a program which has been specially conceived for DewCal®, and that with a minimum power consumption. Possible technical faults are immediately detected by means of target-performance comparisons and reported to the alarm system. The automatic water feed keeps the operating conditions constant on the one hand and on the other, it ensures an operation of the humidifier which is as low-maintenance as possible. All of the gas supply functions including the humidifying are computer controlled with the exception of the manual filling of the storage tank.
 The compact design also enables the DewCal® to be used in small laboratory facilities
The compact design also enables the DewCal® to be used in small laboratory facilities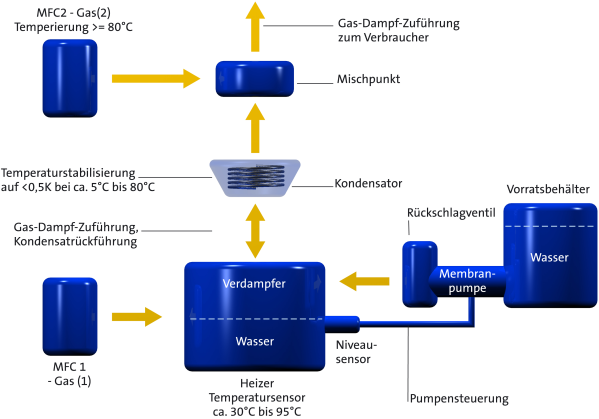 MFC = mass flow controller = Massedurchflussregler
MFC = mass flow controller = MassedurchflussreglerAs this innovation for which Falk Steuerungssysteme GmbH has filed a patent application is based on the measurement of absolutely physical – and easy to measure – parameters, it is possible to adjust the required dew point of gasses much more precisely and faster. This advantage results from the fact that dew point changes simply result in changes being made to the volume flows of dry and moist gas – and basically speaking, the required dew point presents a calculated parameter comprising the volume and the water concentration. As the taking of long adjustment times of sensors into account is no longer necessary, it is now possible to achieve process changes much faster – with corresponding time savings, thereby achieving an increased productivity.
The compact design of the new system also enables it to be use for small laboratory facilities. One application example of an efficient use of DewCal® is the so-called hot dip processes in the treatment of metal surfaces. These systems can be used to exactly transfer the effects of modified gas mixtures, metal alloys or temperatures from a laboratory scale to metal strip processing plants at a later date – for the galvanizing of steel sheets, for example. The background: when steel surfaces are annealed for example, water molecules in process gasses result in the carbon atoms in the metal grid being released so that they can react with the oxygen atoms in the water to form carbon monoxide or carbon dioxide. This decarbonisation modifies the material properties of the used material as a consequence. This effect can only be used in a targeted form in process engineering if the moisture content of gas flows is known. This is why sensors are often used in order to measure the dew point.
As sensors can only be calibrated relative to a reference system however, they are restricted by the measurement errors which occur as a matter of course. This is caused by sensor calibration errors and the temporal changing of its sensitivity. Moisture sensors normally display a hysteresis. Their time content therefore depends on the preceding sign of a vapour pressure change. Especially long adjustment times can be observed when the dew point is lowered and at low dew points. If gasses should be loaded with vapours other than water vapour, relative calibrated systems additionally require a corresponding matching sensor for the measuring of the vapour density.
The author Thorsten Sienk is a freelance specialized journalist from Bodenwerder.
Internet: www.sienk.de
document download (pdf, german)
 In many applications, the moisture content of the process gasses has to be precisely defined
In many applications, the moisture content of the process gasses has to be precisely defined
